AI Thinking Illusion: Apple vs Anthropic Debate

Today, I want to dive into one of the hottest topics in the world of AI. You’ve probably heard about the new generation of language models — OpenAI o3 pro, Claude 4 Sonnet Thinking, Deepseek R1, and others. They are called “reasoning models” (Large Reasoning Models, LRM), and they promise not just to answer questions, but to show their entire “thought process,” breaking down the task step by step. Sounds like a breakthrough, right? Almost like the birth of true artificial intelligence.

But what if I told you that this might be just a very convincing illusion?

I stumbled upon a fresh and, frankly, sobering research titled “The Illusion of Thought” from a group of engineers at Apple. They decided not to take bold announcements at face value and dug deeper. Instead of running models through standard tests, they created a real “intellectual gym” with puzzles for them. And what they discovered casts doubt on the very nature of these systems’ “thinking.”

Let’s break down together what happened there.

Why Math Tests Are a Bad Metric

First of all, it's important to understand why researchers doubted standard benchmarks in the first place. Most models are tested on mathematical and coding tasks. The problem is that the internet is flooded with solutions to these tasks. The model, like a diligent but not very clever student, could have simply “memorized” millions of examples during training. This is called data contamination, and the following results from mathematical tests illustrate this well.

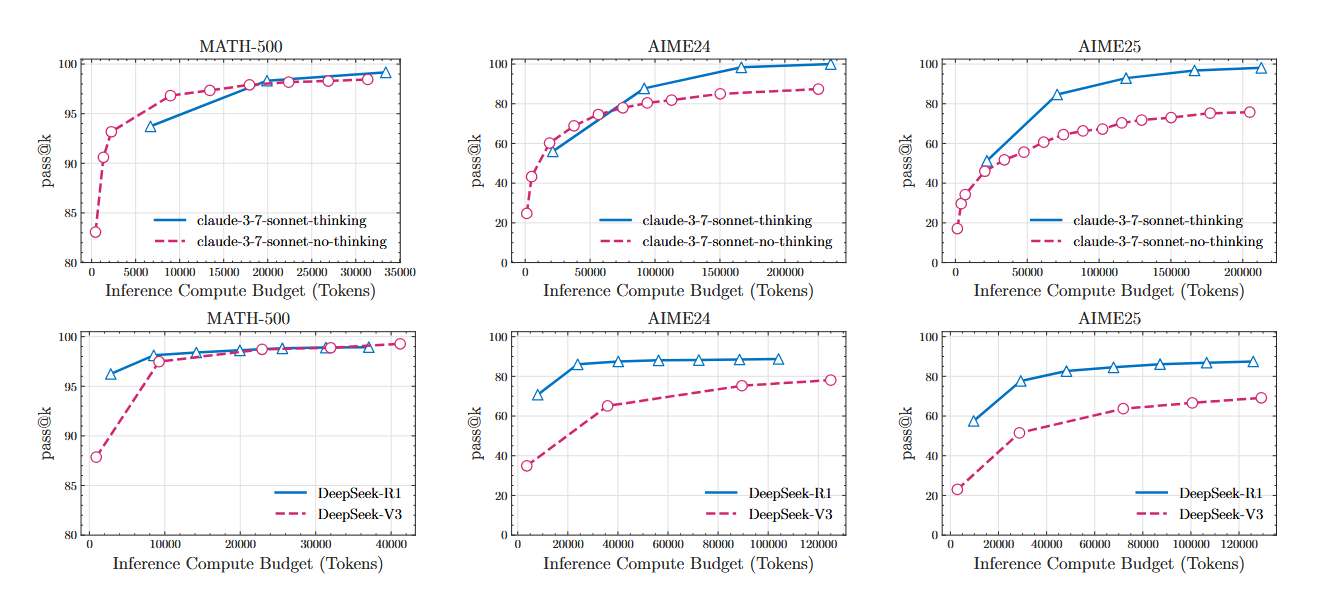
Pasted image 20250616192539.png — Comparative analysis of reasoning and non-reasoning models in various mathematical benchmarks reveals inconsistent performance patterns. While results on the MATH-500 dataset show comparable performance between both types of models, reasoning models demonstrate superior performance on AIME24 and AIME25 benchmarks. Furthermore, the observed decline in performance from AIME24 to AIME25 highlights the vulnerability of these benchmarks to data contamination issues.

How do you check if a student truly understands physics, rather than just memorizing formulas? You need to give them a task they’ve never seen before.

This is exactly what Apple did. They took four classic puzzles:

Tower of Hanoi: A puzzle with three rods and a set of disks of different sizes. The goal is to move all disks from the first rod to the third. Only one disk can be moved at a time, only the top disk can be taken, and a larger disk can never be placed on a smaller one.
Checker Jumping: A one-dimensional puzzle where red and blue checkers and one empty space are arranged in a row. The task is to swap all red and blue checkers. A checker can be moved to an adjacent empty space or jumped over one checker of a different color to an empty space. Backward movement is prohibited.
River Crossing: A puzzle where n actors and their n agents must cross a river in a boat. The goal is to transport everyone from the left bank to the right. The boat has limited capacity and cannot sail empty. An actor cannot be in the presence of another agent without their own. Similar to our "Wolf, Goat, and Cabbage" puzzle.
Blocks World: A puzzle with stacks of blocks that need to be rearranged from an initial state to a target state. The task is to find the minimum number of moves to do this. Only the topmost block in any stack can be moved, placing it either on an empty space or on another block.

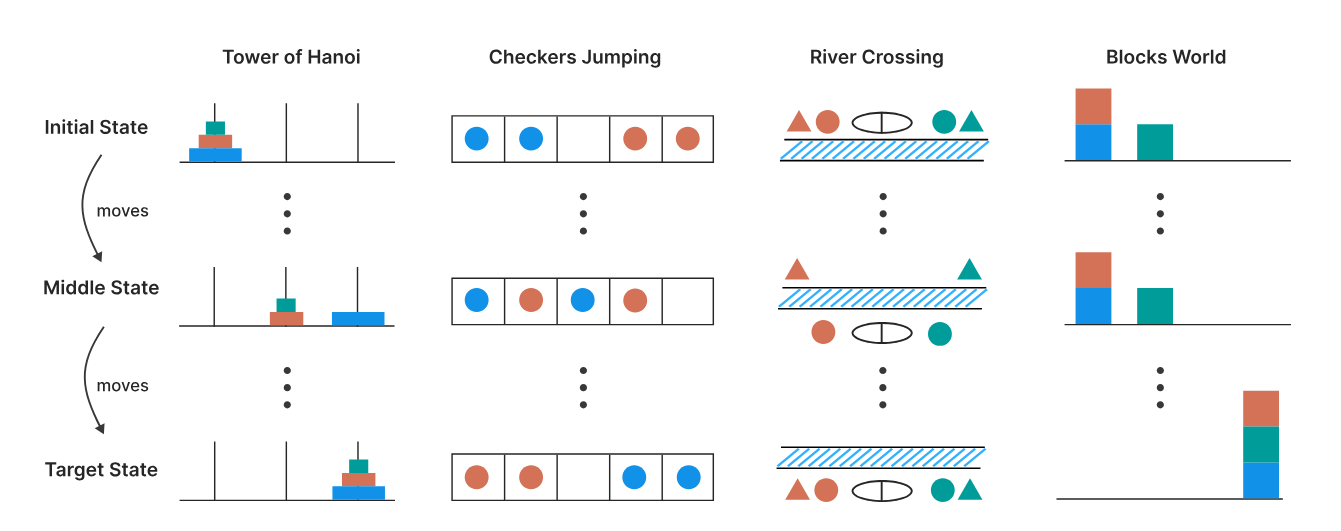
Pasted image 20250616185719.png — Illustration of the four puzzle environments. Columns show progression from an initial state (top) through an intermediate state (middle) to a target state (bottom) for the puzzles: Tower of Hanoi, Checker Jumping, River Crossing, and Blocks World.

The beauty of these puzzles is that their difficulty can be precisely controlled simply by changing the number of elements (disks, checkers, blocks). At the same time, the logic of the solution remains the same. This is an ideal environment to see where a model’s “reasoning” breaks down.

Three Difficulty Modes: From Genius to Complete Failure

After running these puzzles through "thinking" models and their ordinary, "non-thinking" counterparts (e.g., Claude 3.7 Sonnet Thinking vs. Claude 3.7 Sonnet), researchers discovered a clear and reproducible pattern that can be divided into three modes.

1. Low Complexity Mode: Yellow Zone On simple tasks, requiring only a few moves, regular models performed just as well, and sometimes better, than their "thinking" counterparts. Moreover, they used significantly fewer computational resources. Essentially, making a reasoning model solve a simple task is almost like using a supercomputer to add 2+2. The "thought process" here is an excessive luxury that only slows down the work.

2. Medium Complexity Mode: Blue Zone This is where "thinking" models began to shine. When the task became sufficiently tangled, the ability to generate a long chain of reasoning, test hypotheses, and self-correct gave them a clear advantage. The gap in accuracy between reasoning and non-reasoning versions became significant. It seemed like, here it was — the proof!

3. High Complexity Mode: Red Zone But the triumph was short-lived. As soon as the puzzle's complexity crossed a certain threshold, something astonishing happened: the performance of both models dropped to zero. A complete collapse.

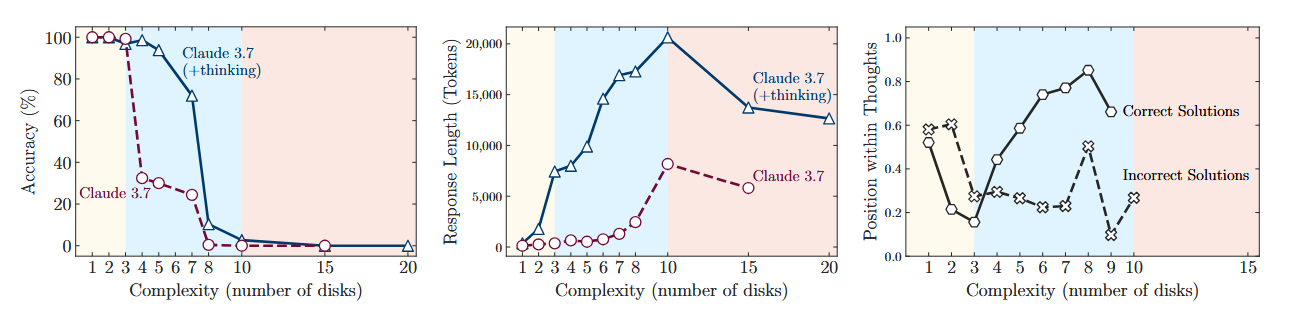
Pasted image 20250616190039.png — Left and middle: At low complexity, non-reasoning models are more accurate and token-efficient. As complexity increases, reasoning models outperform them but require more tokens — until both collapse beyond a critical threshold. Bottom right: For correctly solved tasks, Claude 3.7 Thinking typically finds answers early at low complexity and later at higher complexity. In cases of failure, it often gets stuck on an early incorrect answer, wasting the remaining token budget. Both cases reveal inefficiencies in the reasoning process.

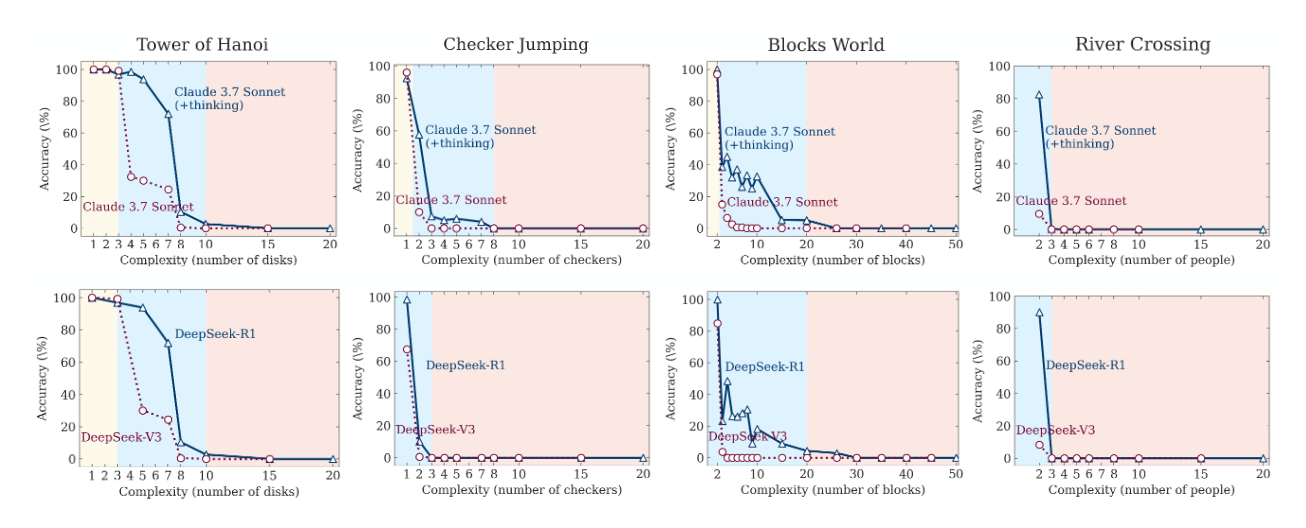
Pasted image 20250616193421.png — Accuracy of reasoning models (Claude 3.7 Sonnet Thinking, DeepSeek-R1) compared to their non-reasoning counterparts (Claude 3.7 Sonnet, DeepSeek-V3) across all puzzle environments and different task complexity levels.

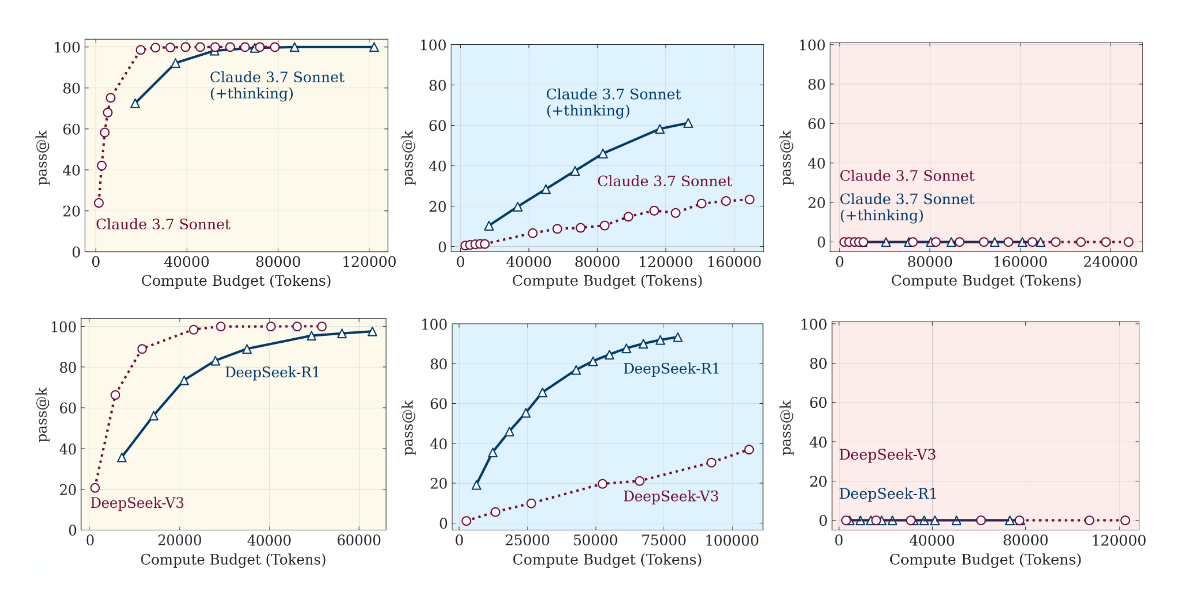
Pasted image 20250616193507.png — Performance Pass@k of reasoning versus non-reasoning models at equivalent computational budgets in low, medium, and high complexity puzzle environments. Non-reasoning models show superior results in simple tasks, reasoning models demonstrate advantages at medium complexity, while both approaches fail at high complexity regardless of computational resource allocation.

Yes, "thinking" models lasted a little longer and gave up a few steps later. But ultimately, they hit the same fundamental wall. Their reasoning ability was not truly generalizable. It simply delayed the inevitable failure.

The Paradox of the Surrendering Mind

But the strangest and most counterintuitive discovery awaited the researchers when they looked at how much the model "thinks" depending on the complexity. It's logical to assume that the more complex the task, the more effort (thinking tokens) the model should spend on it.

And at first, that was true. As complexity increased, so did the amount of "thinking." But only up to the point where the collapse began. Approaching critical complexity, the models behaved paradoxically: they started to reduce their efforts, which is clearly visible in the graph.

Pasted image 20250616193754.png — Accuracy and reasoning tokens versus task complexity for reasoning models in various puzzle environments. As complexity increases, reasoning models initially expend more tokens while accuracy gradually declines, until a critical point where reasoning collapses — performance sharply drops, and reasoning effort decreases.

Imagine a student taking an exam who, seeing a too-complex problem, doesn't try to fill several pages of scratch paper, but just looks at it for a couple of seconds and submits a blank sheet. And they have both time and paper. The models, having a huge reserve in generation length, simply stopped trying.

This points to a fundamental limitation of their architecture. It's not just a lack of knowledge, but some built-in limit to scaling cognitive effort.

Two Nails in the Coffin of “Pure Reason”

If the previous points still left room for interpretation, the following two conclusions look like a death sentence for the idea that LRMs truly "understand" logic.

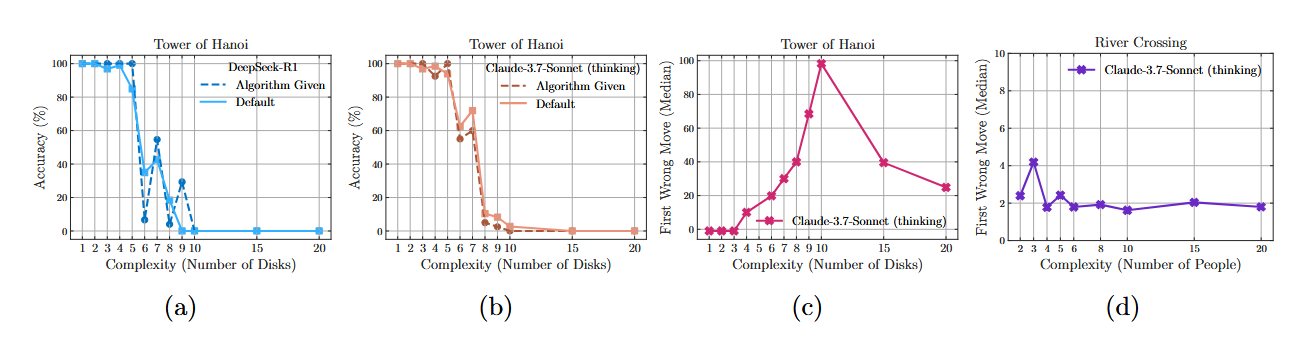
1. Inability to follow instructions This is perhaps the most damning argument. Researchers conducted an experiment with the Tower of Hanoi, in which they gave the model a precise step-by-step solution algorithm directly in the prompt. The model was only required to do one thing — blindly follow the instructions.

The result? No improvement. The model failed at the exact same level of complexity as it did without the hint. This can be compared to a person who was given a very detailed instruction manual for assembling an IKEA cabinet, but still can't put it together. Such behavior suggests that they are not reading and following the steps, but trying to recreate what they've seen before from memory or from a picture. It seems the model is not executing the algorithm, but trying to recognize a familiar pattern.

2. Strange selectivity The analysis revealed another interesting thing. The Claude 3.7 Sonnet Thinking model could solve the Tower of Hanoi with 5 disks (that's 31 moves) with almost perfect accuracy, but completely failed the River Crossing problem for 3 pairs (only 11 moves).

Why is that? The probable answer is again in the training data. Examples of solving the Tower of Hanoi are plentiful on the internet. But complex variants of River Crossing are much fewer. The model is strong in what it has "seen" many times, and weak in what is new to it, even if the task is logically simpler.

Pasted image 20250616194022.png — **(a) and (b)** Despite providing the solution algorithm in the prompt, execution failures are observed at similar points, highlighting the limitations of reasoning models in executing logical steps. **(c) and (d)** Notably, the Claude 3.7 Sonnet model demonstrates significantly longer error-free sequences in the Tower of Hanoi compared to early failures in the River Crossing scenario.

But the story didn't end there. A Counter-Punch from Claude's Creators

It seemed that the conclusions were clear: "thinking" models were a very advanced, yet still an illusion. I had almost finished writing this article when, like in a good detective story, a new witness appeared on the scene and turned the whole case upside down. In the form of a response publication boldly titled “The Illusion of the Illusion of Reasoning,” researchers from Anthropic (creators of Claude) and Open Philanthropy entered the arena.

This was not just a comment; it was a complete dismantling. The essence of their reply is simple and merciless: Apple's conclusions speak not about fundamental limitations of the models, but about fundamental errors in the design of the experiment itself. Let's see how they dissect Apple's arguments.

1. The first nail in the coffin of "reasoning collapse": ran out of paper, not thoughts. Remember the idea that models "gave up" on complex tasks? Anthropic claims: models didn't give up, they simply hit a token limit. This is not a student who abandoned solving a problem, but a student who was given only one sheet of paper. When it runs out, they write "and so on" and turn in their work. The models did the same, literally stating in their answers: "The pattern continues, but to avoid making the answer too long, I will stop here." Apple's automated test, unable to read such nuances, counted this as a failure.

2. The second shot: drama with an unsolvable problem. And here begins a real detective story. Researchers from Anthropic checked the conditions of the River Crossing problem and found that for 6 or more pairs of actors/agents with a boat capacity of 3 people, it is mathematically unsolvable. This is a known fact, confirmed by another study. It turns out that Apple was seriously giving models a "fail" for not being able to solve an unsolvable problem. This is like punishing a calculator for giving an error when dividing by zero.

3. And finally, the finishing blow: ask for a recipe, not slicing. To definitively prove their point, the Anthropic team changed the question itself. Instead of requiring the model to output thousands of moves for the Tower of Hanoi, they asked it to write a program (a Lua function) that generates the solution. And — bingo! — the models that supposedly "collapsed" easily wrote a perfect recursive algorithm. Apple, in essence, was testing the mechanical endurance of the model by forcing it to "slice vegetables" for a huge banquet. Anthropic, however, tested its knowledge of the process by asking it to "write a recipe." And the model knew it.

So who is right? The illusion of reasoning or the illusion of evaluation?

This counter-punch completely shifts the balance of power. Now, Apple's conclusions look not like a discovery of a fundamental flaw in AI, but as a demonstration of a classic research trap, into which it's easy to fall if you don't check your own initial data.

It turns out that the very "wall of complexity" that the models ran into was not built by them, but by the experimenters themselves through artificial limitations and impossible conditions.

The biting but fair verdict from Anthropic summarizes this whole story: “The question is not whether models can reason, but whether our tests can distinguish reasoning from typing.”

This story is an excellent reminder that in the world of AI, one must doubt not only the answers of machines but also one's own questions. I am sure that many of us have encountered this in our practice. Sometimes it seems that the model is "acting dumb," but in reality, we simply asked the question in a way that prevents it from giving a good answer within the given constraints.

What do you think about this dispute? Whose arguments do you find more convincing? Have you ever had cases where you yourself misjudged the capabilities of AI simply because the "test" was incorrectly designed?